[알고리즘] 활동 선택 문제 / Activity Selection Problem

활동 선택 문제는 시작 시간과 종료 시간이 주어진 다양한 활동 중에서 가장 많은 활동을 할 수 있는 활동의 집합을 고르는 문제이다.
활동의 정보를 보고 활동 간의 관계를 계산하여 가장 긴 활동들의 sequence를 구한다.
이 문제는 순간의 최적을 전체의 최적이라고 판단하는 그리디 알고리즘으로 구할 수 있는데, 가장 빨리 끝나는 (=종료 시간이 가장 빠른) 활동을 선택하여, 남는 시간이 가장 크도록 하는 활동들을 최적이라고 판단하여 선택한다. 그리디 알고리즘의 개념은 아래 게시물에 잘 설명되어 있다.
가장 짧은 활동, 가장 덜 겹치는 활동, 일찍 시작하는 활동을 선택할 경우 반례가 존재해 문제 전체로 봤을 때 최적의 해를 구할 수 없게 되기 때문이다.
수열 S = {1, 2, … , n}을 종료 시간 순으로 설정된 활동의 집합이라고 한다.

[알고리즘] 그리디 알고리즘 / Greedy Algorithm

 

 

이것은  활동 선택 문제의 최적해를 구하는 activity_selection pseudocode이다.
여기서 s와 f는 각각 i, j번째 활동의 시작 시간과 종료 시간을 담은 배열이며, A믄 선택된 활동(정답 sequence)이다.
i=2부터 활동의 개수만큼 반복문을 돌리면서, 특정 활동의 시작시간이 다른 활동의 종료 시간보다 크거나 같으면 이어붙일 수 있는 활동이므로(sequence가 만들어지므로) A에 해당 활동을 추가해주고, j에 i를 대입해준다.
반복문이 종료되면, 결과 A를 반환한다.

활동을 종료 시간에 따라 오름차순 정렬하고, 그 목록을 스캔하고 현재 선택 항목과 호환되는 경우 해당 활동을 선택한다.
즉, 현재 시간을 기준으로 할 수 있는 끝나는 시간이 가장 빠른 활동을 계속 결과에 추가해준다.
따라서 동작 시간은 정렬하는 시간에 Theta(n)을 더한 값이며, 따라서 시간 복잡도는 Theta(n)을 갖게 된다.

이러한 시작 시간과 종료 시간을 가진 11개의 활동들이 있다고 가정하자.
이 활동들은 종료 시간 순으로 활동들이 정렬된 상태이다.

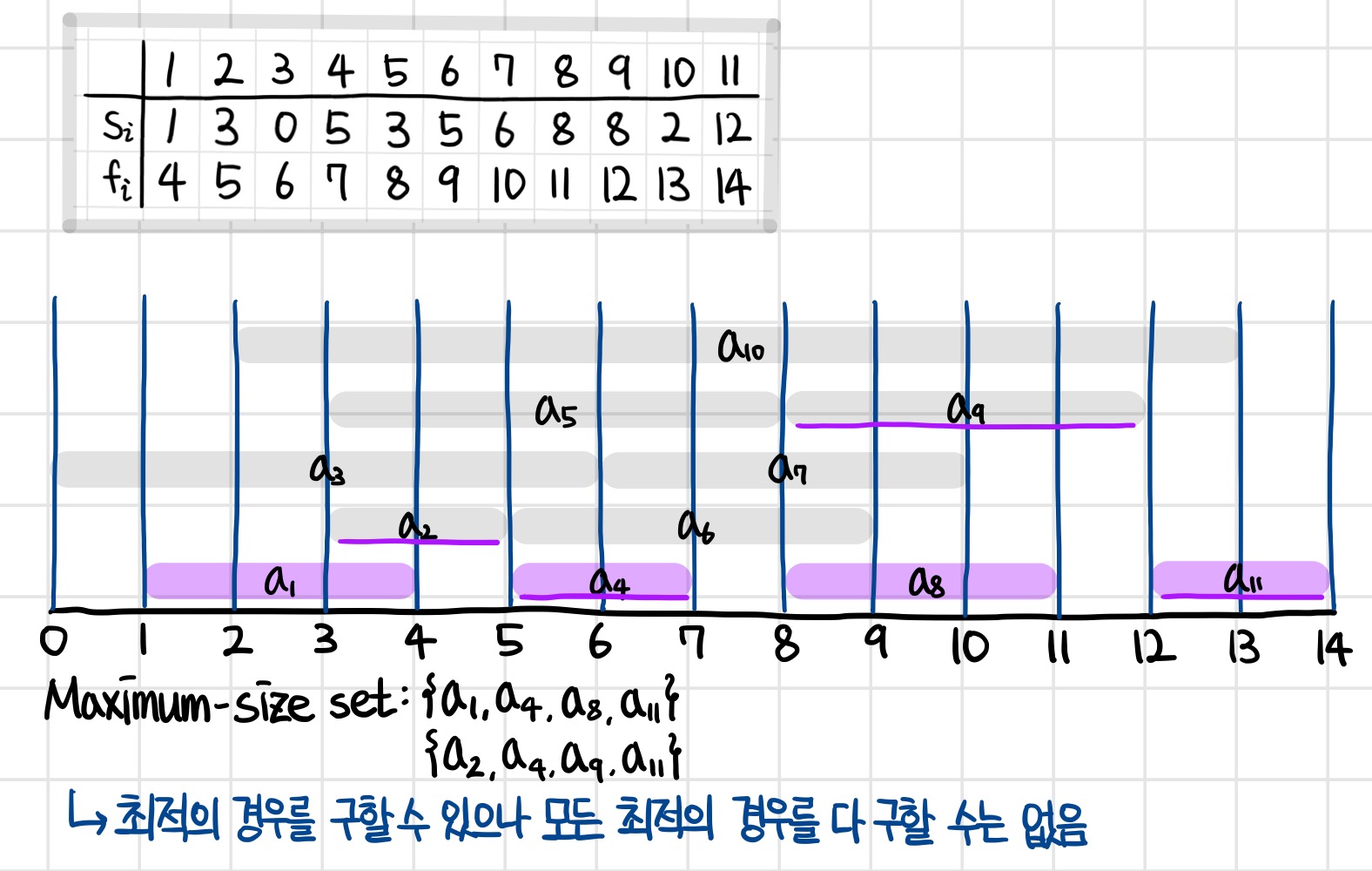
이처럼 활동을 시각화하여 나타내면 다음과 같다.
종료 시간이 가장 짧은 a1을 처음으로 선택하고, 시작 시간이 a1의 종료시간 뒤에 있는 활동 중 종료시간이 가장 빠른 a4를 다음으로 선택한다.
같은 과정을 반복하여, a1, a4, a8, a11을 선택하는 4개의 활동을 선택할 수 있다.
이때, a2, a4, a9, a11의 수열도 길이가 4인 sequence를 만족하는 것을 볼 수 있는데, 여기서 알 수 있듯 최적의 경우를 구할 수는 있지만, 모든 최적의 경우를 다 구할 수는 없는 특징을 볼 수 있다.
최적해가 몇인지 구할 수는 있고, 그것을 만족하는 정답을 하나 보여줄 수 있을 뿐, 결과로 나온 최적해를 가지는 다른 방법은 구할 수 없다는 것을 의미한다.
예제의 경우에서는 하나씩 선택하는 과정에서 종료 시간이 빠른 활동을 선택하도록 알고리즘을 구성했고, 따라서 그리디 알고리즘으로는 a2가 선택될 수 없기 때문에 {a2, a4, a9, a11}을 찾지 못하게 되는 것이다.

그렇다면, 그리디 알고리즘으로 구하는 최적해가 정말 문제 전체의 최적이 될 수 있는지 증명해보자.
S = {1, 2, … , n}을 종료 시간 순으로 정렬한 활동의 집합이라고 하고, kn은 n번째 활동의 길이, A는 최종 결과라고 하면,
k1 = 1이면 A는 Greedy Choice, 즉 최적의 선택으로 시작한다.
k1 != 1이면 A’ = (A - {k1}) U {1}. (k1을 빼고 길이가 1인 활동을 넣은 집합)이라고 했을 때, A - {k1}과 {1}은 공통 원소가 존재하지 않는 집합, disjoint이다.
그렇다면 활동 A’은 활동 {1}과 호환이 가능하므로 최적해가 된다.
A’는 최적해이므로 A’과 A의 원소의 개수는 같다.
그러므로, 활동 선택 문제를 그리디 알고리즘으로 동작시켰을 때 최적해가 항상 존재한다는 결론을 얻을 수 있다.