
점근 표기법, Asymptotic Notation을 활용해 우리는 극한(입력값 n이 충분히 클 때)에서 함수의 동작을 설명할 수 있습니다. 주로 시간 복잡도(Time Complexity)에서 사용합니다.
특정 함수를 다른 함수들을 통해 비교하여 그 특정 함수가 어느 정도 범위를 가질지 예측하는 것으로
이것을 통해, 알고리즘의 우열을 구할 수 있고 어떤 알고리즘이 더 효율적인지 분석할 수 있습니다.
예를 들어, T(n) = 10n^2 + 7n + 102라고 하면
낮은 차수의 항을 삭제하고, 최고차항의 계수를 지워 n^2으로 나타냅니다.
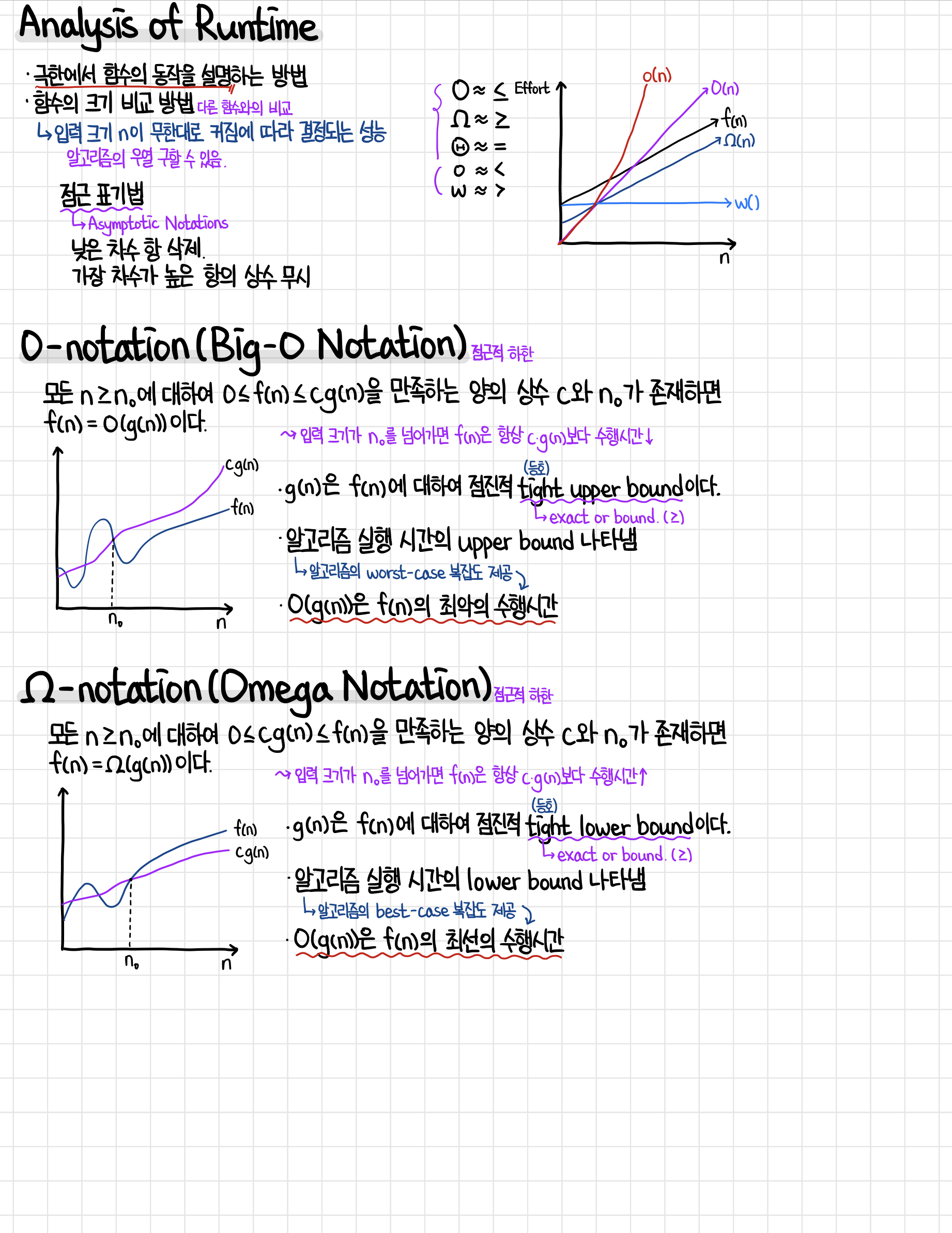
Big-O Notation


가장 많이 사용되는 점근표기법, 빅 오 표기법(Big-O notation)입니다.
필기 사진에 나와있듯, 빅오 표기는 f(n) = O(g(n)) 과 같이 표시하는데,
이때 g(n)을 함수 f(n)의 점근적 상한(Asymptotic Upper Bound)이라고 합니다.
즉, f(n)의 복잡도는 알고리즘 성능이 최악의 경우라도 항상 g(n)보다 작거나 같다는 의미가 됩니다.
따라서 함수 괄호 안에 있는 식의 계수가 낮을수록 효율적입니다.
그래프를 보면, f(n)이 아래에 위치해 있게 되는데, 세로축이 시간을 의미하기 때문에 최악의 경우, 그래프가 위로 올라가도 g(n)의 시간복잡도 보다 낮다는 의미가 되므로
최악의 경우에서 시간복잡도를 나타낼 수 있게 됩니다.
Omega Notation


Big-O가 최악의 경우 시간 복잡도를 설명한다면, Omega notation은 점근적 하한으로 최선의 경우 시간 복잡도를 설명합니다.
그렇기 때문에 효율적인 순서가 Big-O notation의 역순입니다.
Big-O notation과 유사한데, 수식과 그래프를 보면 f(n)과 g(n)의 관계가 반대로 되어 있습니다.
즉, 아무리 f(n)이 최선의 수행시간을 갖는다고 하더라도, g(n)보다는 느리게 된다는 말이며, 따라서 알고리즘의 best-case를 설명할 수 있는 표기법입니다.
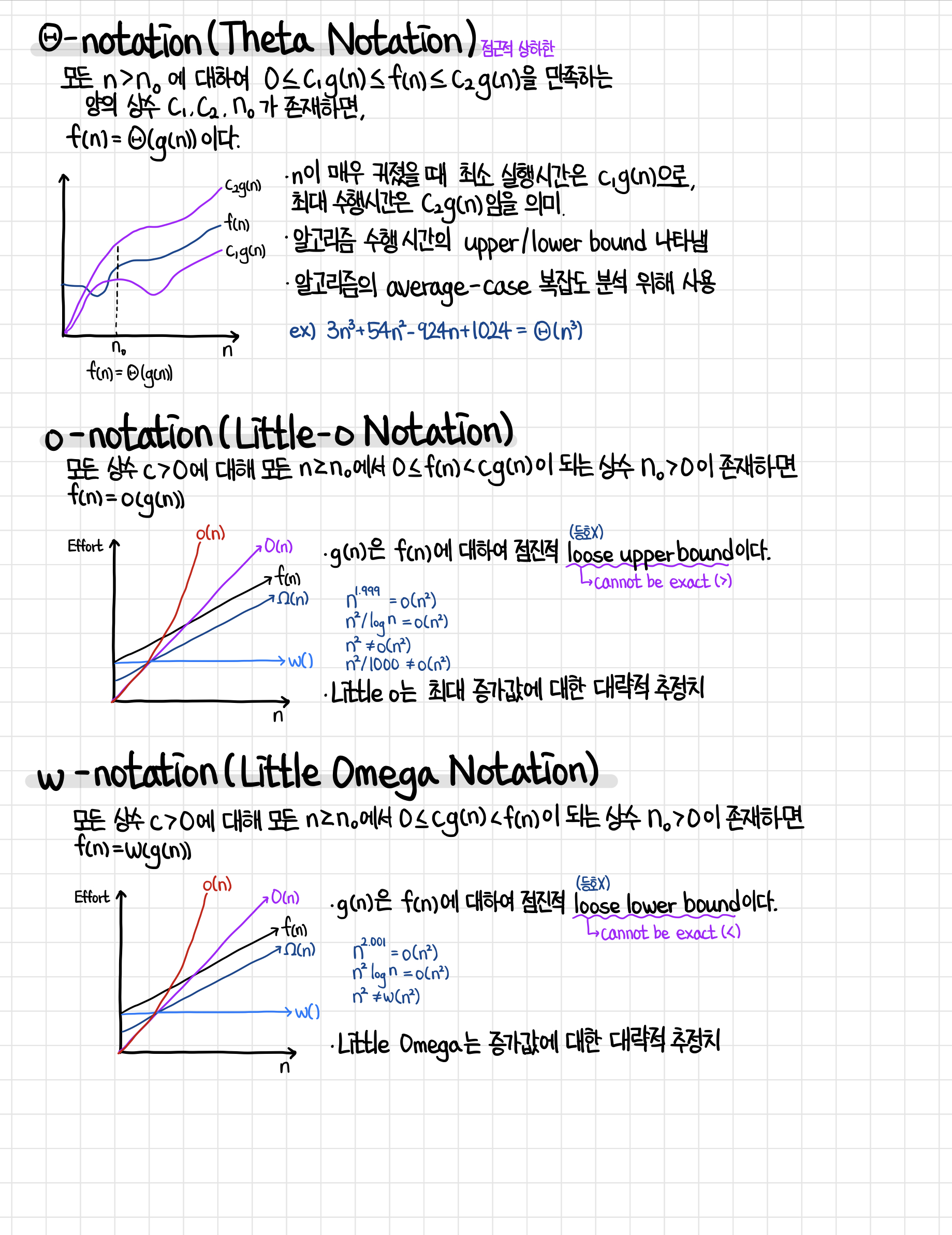
Theta Notation


앞서 설명한 Big-O와 Omega를 한 번에 설명하는, Theta notation입니다.
Theta notation은 점근적 상하한으로, 마치 Big-O와 Omega notation을 한 번에 충족시키는 느낌으로 최선 또는 최악의 경우 모두 g(n)의 범위 내에 있다는 것입니다.
이러한 특성으로, Theta Notation은 평균적인 복잡도를 나타낼 수 있습니다.
Little-o Notation

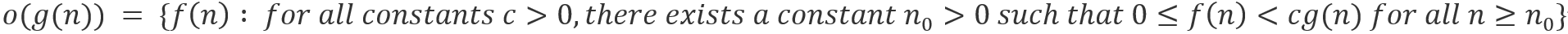
Little-o notation은 최대 증가값에 대한 대략적 추정치로, Big-O 표기법과 유사한데, 수식에서 등호가 하나 빠진 형태입니다. 또한 Big-O에서의 ‘어떤 상수 c 하나가 존재하면’이 아니라, Little-o는 ‘모든 상수 c’에 대하여 성립해야 합니다. 위 사진에서 예시를 보면 쉽게 이해할 수 있습니다.
n^1.999가 n^2와 절대 같아질 수는 없지만, 근사적으로는 같다고 볼 수 있습니다. 이때 n^1.999는 근사적으로 n^2와 같으면서 살짝 작으므로, n^1.999 = o(n^2)와 같이 나타낼 수 있는 것입니다.
Little-omega Notation
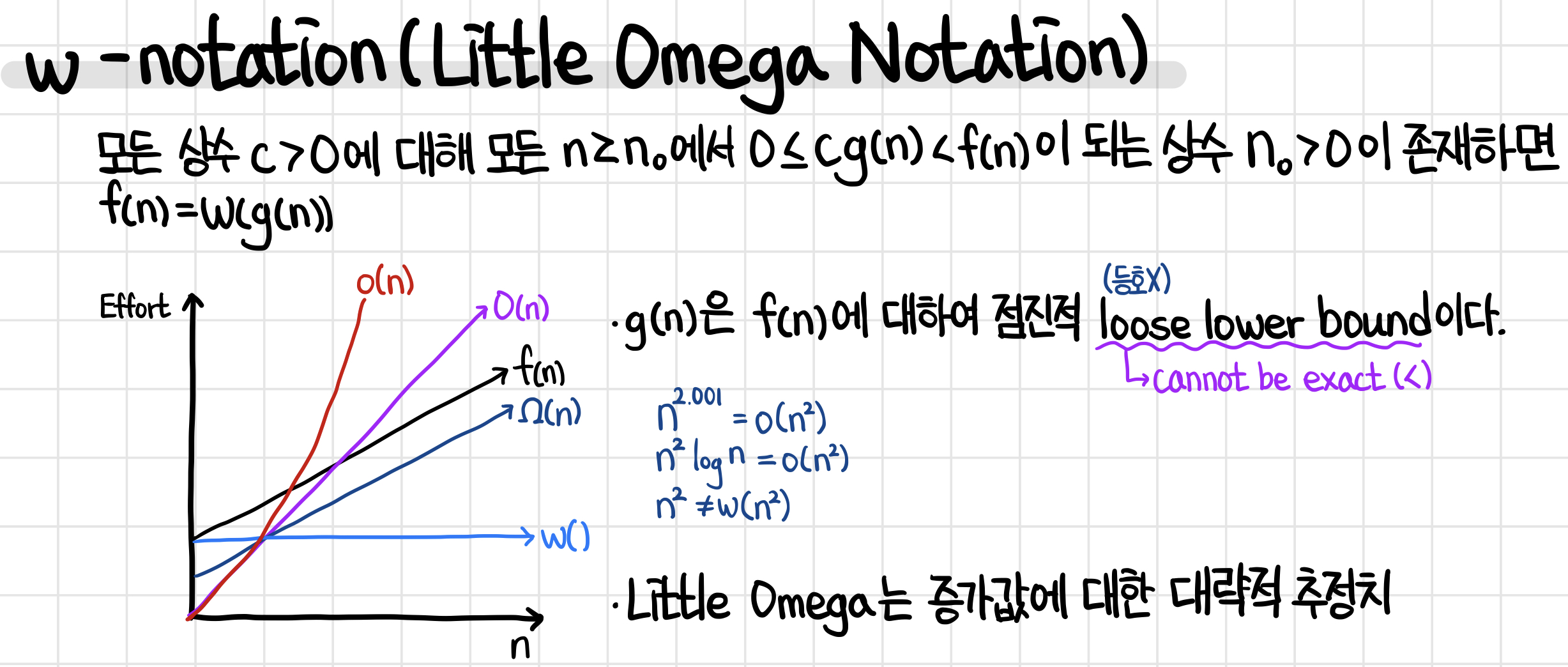
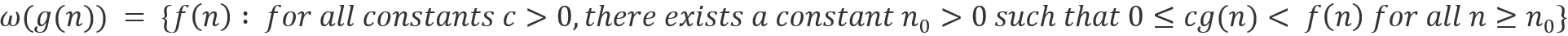
Little-omega notation은 증가값에 대한 대략적 추정치로, Omega 표기법과 유사합니다. Little-o에서 설명했던 것과 비슷하게 모든 상수 c에 대하여 조건을 만족할 때 표기할 수 있습니다. 마찬가지 예시로 n^2.001은 n^2와 근사적으로 같으나 살짝 크기 때문에 n^2.001 = w(n^2) (컴퓨터 수리 후 오메가로 수정 예정)와 같이 나타낼 수 있습니다.
Properties of Asymptotic Notations
마지막으로, 점근표기법의 성질은 아래와 같습니다.
(함수 f(n), g(n)은 항상 양이라고 가정)


'알고리즘' 카테고리의 다른 글
| [알고리즘] Prim's Algorithm (필기자료) (1) | 2023.10.18 |
|---|---|
| [알고리즘] Graphs (필기자료) (0) | 2023.10.18 |
| [알고리즘] 배낭 문제 / Knapsack Problem (Fractional, 0-1) (0) | 2022.10.31 |
| [알고리즘] 마스터 정리 The Master Method (0) | 2022.10.19 |
| [알고리즘] 재귀 트리 Recursion Tree (0) | 2022.10.17 |