
연쇄행렬곱셈 문제는 행렬곱의 횟수를 최소로 할 때의 최적 답안과 그 횟수를 구하는 문제이다.
행렬을 곱할 때에는 한 번에 두 행렬끼리만 곱할 수 있는데, 여러 행렬을 곱해 답을 구하는 과정에서, 어떠한 행렬쌍을 먼저 곱하는지에 따라 연산의 횟수가 달라지게 된다.
예를 들어 A는 2x3 행렬, B는 3x5 행렬, C는 5x2 행렬이라고 가정했을 때,
((A B) C)는 50회, (A (B C))는 42회가 나오는 것처럼 괄호의 위치에 따라 연산 횟수가 다르게 나온다.
따라서, 가장 적은 횟수로 최종 행렬곱을 구하는 방법을 구하는 것이 연쇄 행렬 곱셈이다.

이 계산을 하기 위해 일일이 하나하나 곱해가면서 값을 비교해 최솟값을 구한다면,
위에 보이는 식과 같이 기하급수적으로 값이 (시간복잡도가) 커지게 된다.
(위 식의 카탈랑 수는 정수론에서 다루는 내용이므로 자세하게 서술하지는 않겠다. 다만 여기서는 값이 매우 커진다고 이해하고 넘어가자.)

이렇듯 하나하나 계산하면 너무 많은 시간이 소요되므로, 이 문제는 상위 문제를 하위 문제로 쪼개고, 그 하위 문제를 저장해놓고 그 값을 이용해 상위 문제를 푸는 기법인 Bottom-up 방식의 동적 프로그래밍으로 해결한다.
i와 j 사이에 있는 특정값인 k를 사용하여 정답을 찾아간다.
연쇄 행렬 곱셈에서는 m[i,j] = min{m[i, k] + n[k+1,j] + p(i-1)p(k)p(j)} 라는 식으로 문제를 해결하는데,
i = j이면 이 자체로 하나의 행렬이므로 행렬곱은 0이고,
i < j 일 때는 i <= k < j인 k를 선택하여 나눈 다음 하위 문제를 이용하여 계산한다.
예를 들어, i와 j가 각각 1과 2라면 k가 1로 하나겠지만, i와 j가 각각 1과 3이라면 k는 1과 2의 2개가 된다.
이때 k가 1일때의 행렬곱 m[1, 3]값과 k=2일 때의 행렬곱 m[1,3] 중 작은 값이 m[1,3]으로 정해진다는 뜻이다.

이 문제를 해결하는 pseudocode이다.
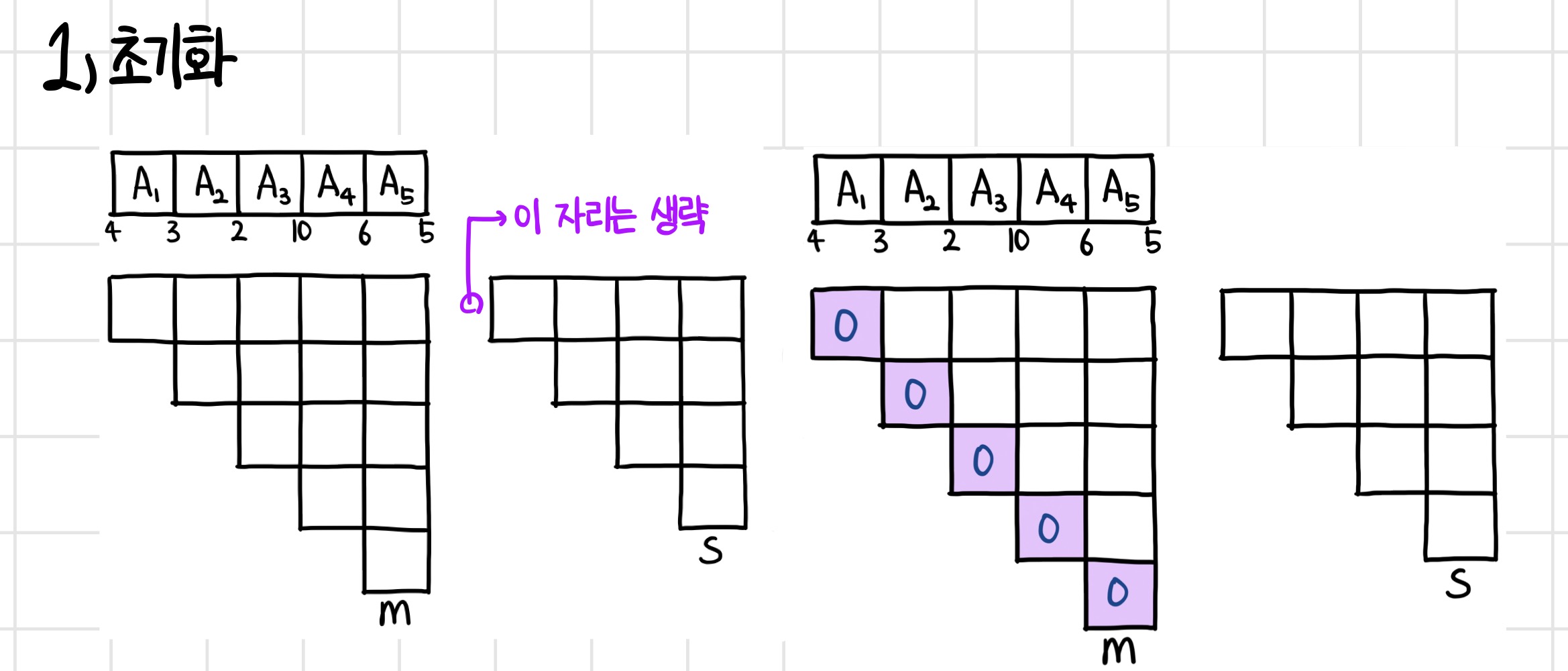
문제 해결을 위하여, 다음과 같은 테이블을 작성한다.
A1부터 A5까지 최소 행렬곱을 구하는 문제로, 위쪽 직사각형 아래에는 해당 행렬의 행과 열의 수를 적는다. 계산을 할 테이블 자리의 인디케이터라고 생각하면 된다.
m 테이블은 각 자리에서 행렬곱이 일어나는 횟수를, s테이블은 그 자리에서 행렬곱이 최소일 때의 k값을 기록한 테이블이다.
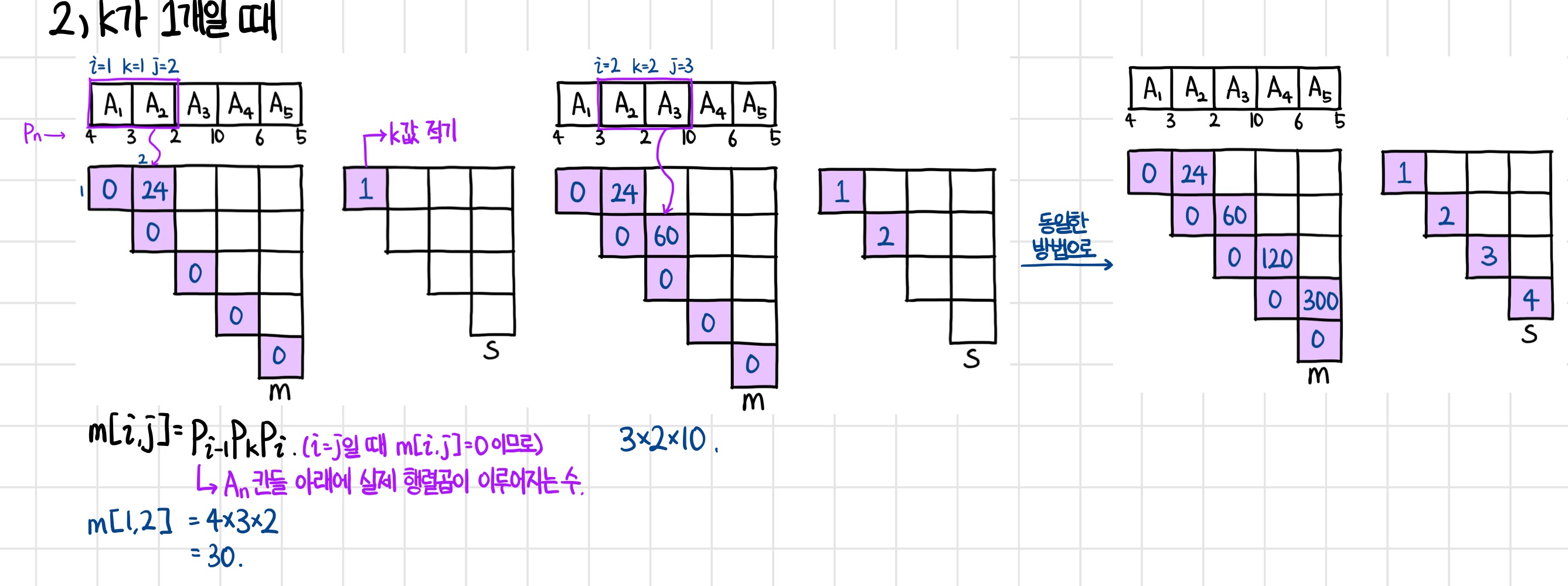
본격적으로 계산을 시작해보자.
k가 1개일 경우에는 m[i,j] = min{m[i, k] + n[k+1,j] + p(i-1)p(k)p(j)}에서 i = k, k+1 = j이므로
m[i,j] = p(i-1)p(k)p(j)만 계산한다.
따라서 k값을 s테이블에 적어주고, 행렬곱을 n-1번 해주고 행렬곱의 결과값을 m테이블에 적으면 된다.
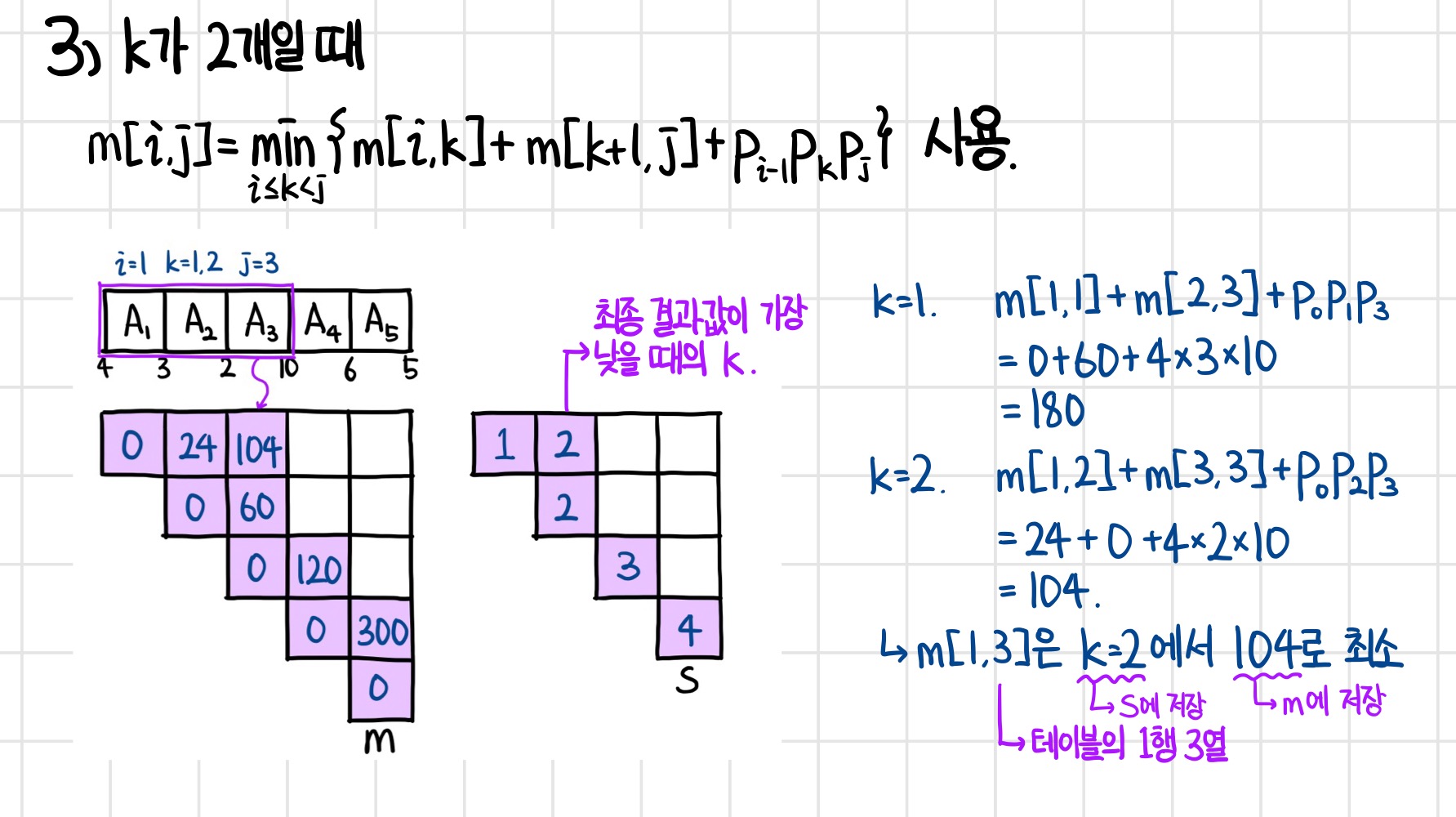
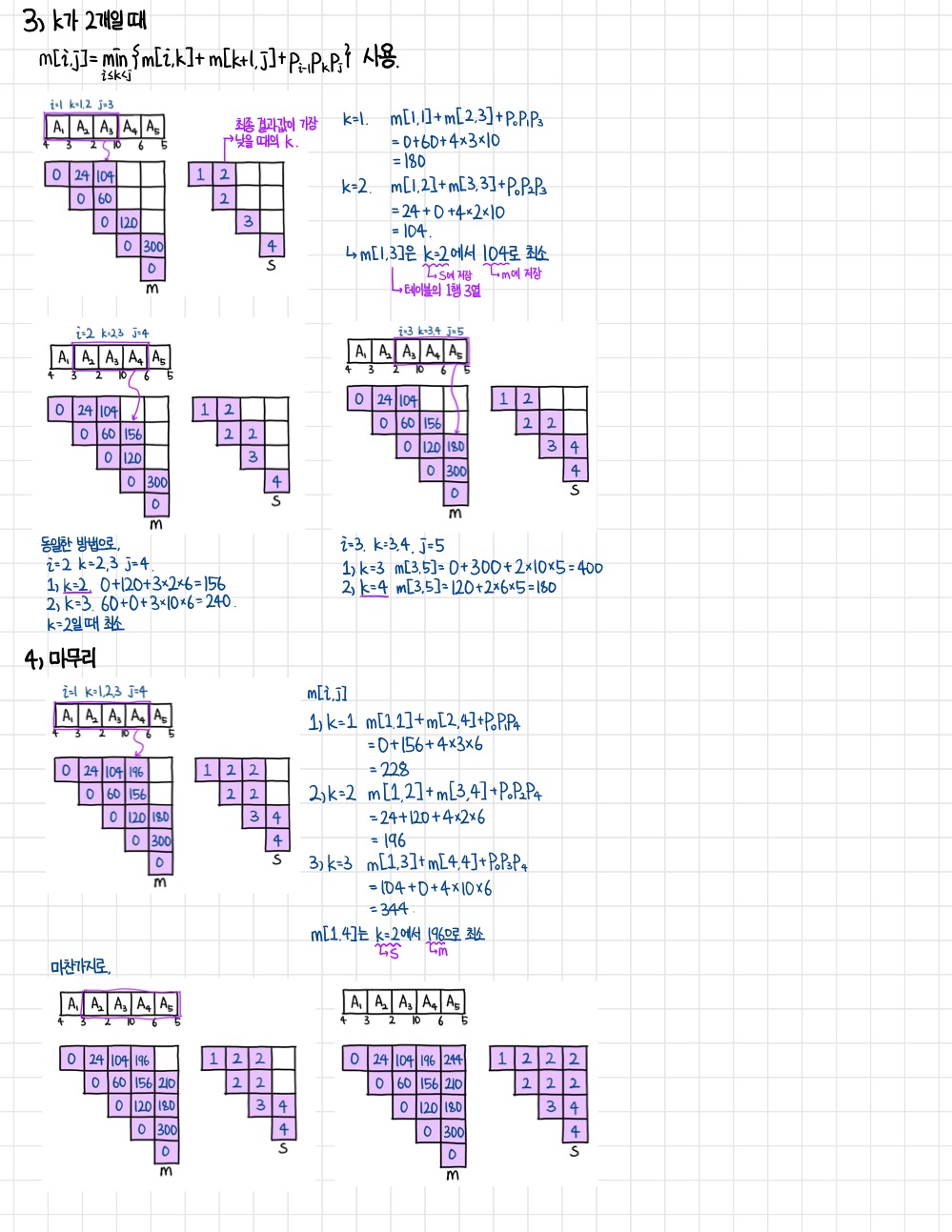
k가 2일 때부터는 전체 식이 모두 필요한데, 지금과 같이 A1 A2 A3에서 (A1 A2) A3가 최소인지, A1 (A2 A3)가 최소인지 비교하는 과정이 필요하기 때문이다.
현재 칸에서는 k가 1일 때 180번, 2일때 104번 행렬곱을 수행하므로 (1,3)에서 행렬곱의 수는 104이고, 그 위치에서의 k값은 2가 되어 s테이블에 기록한다.
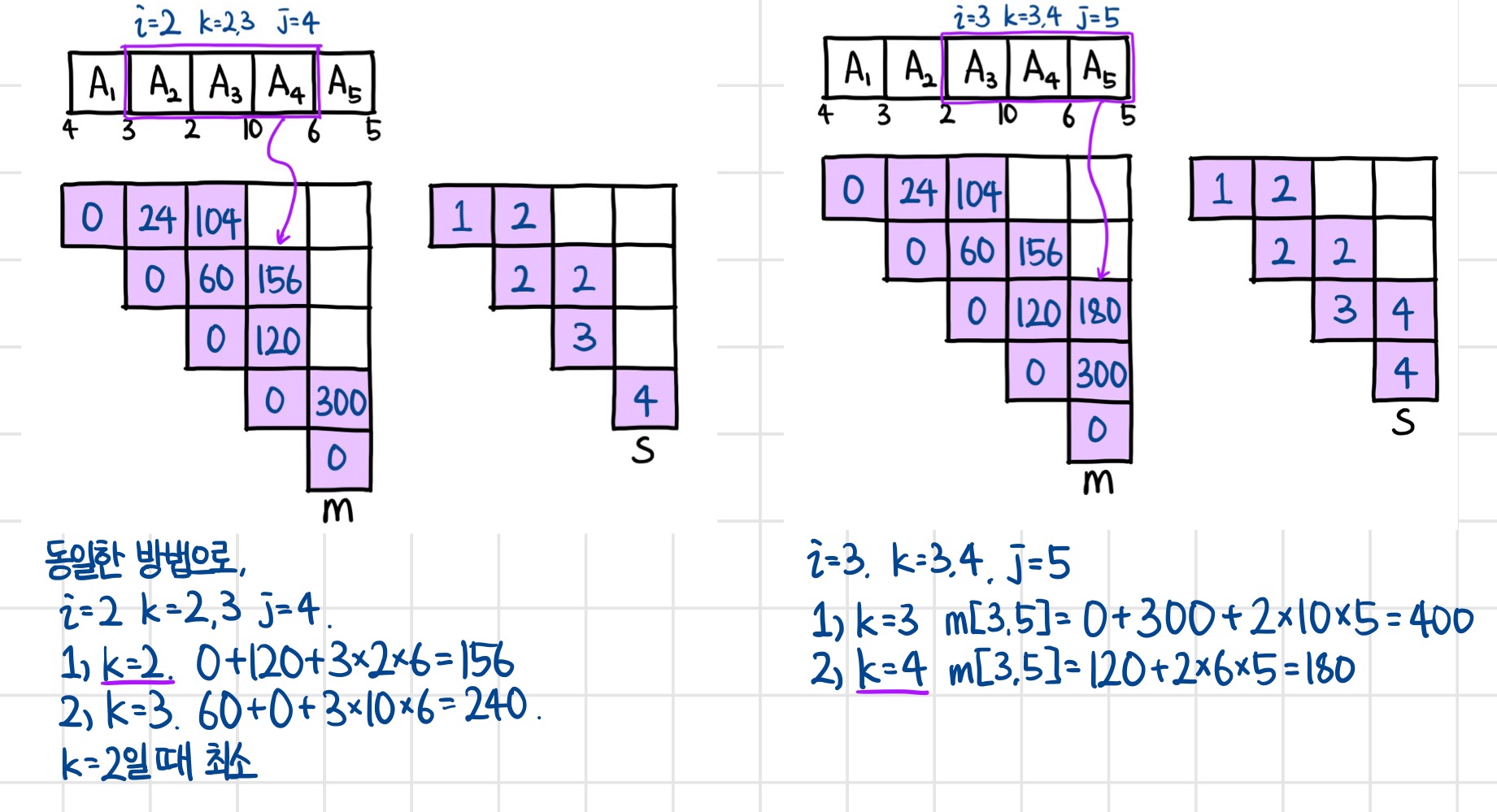
동일한 방법으로 진행해 3개 행렬곱의 최적해를 구하고 그 값을 m테이블에, 그 때의 k값을 s테이블에 기록한다.
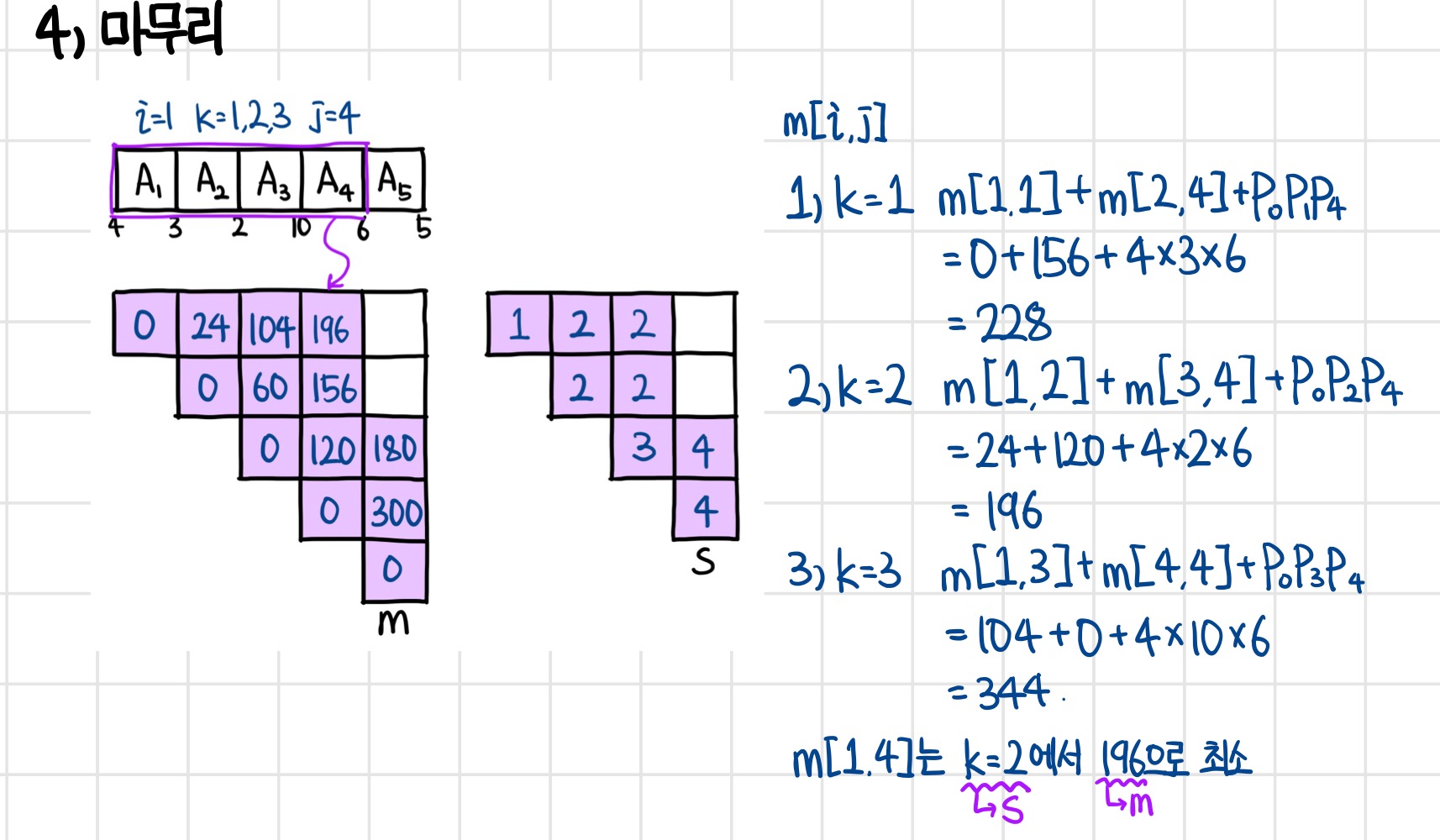
비교할 행렬곱의 개수가 커져도 방법은 똑같다.
같은 식을 사용하여 이전 최적 행렬곱을 이용해 적절한 k값과 행렬곱 값을 구해준다.
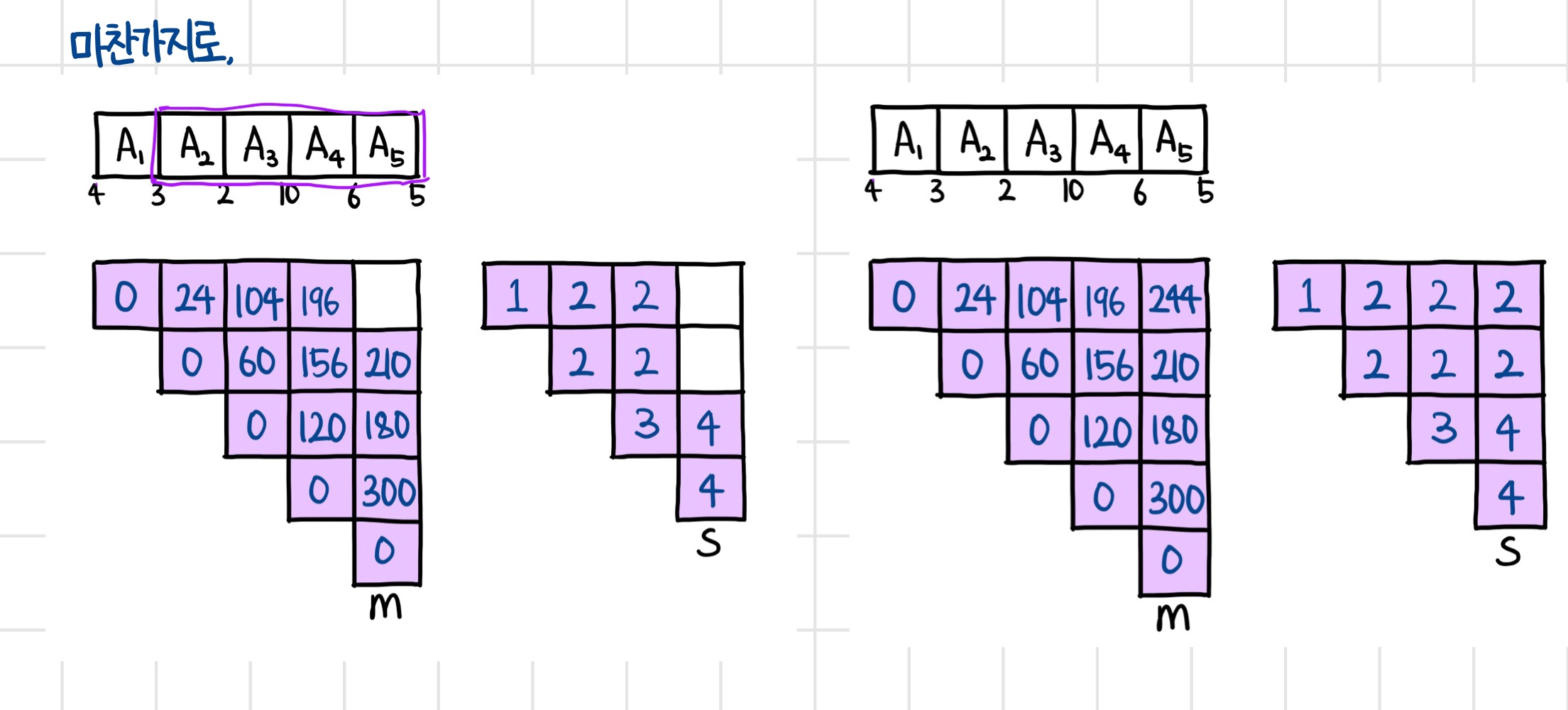
이렇게 해서 예제의 최적행렬곱을 모두 구했다.
이 문제의 최적행렬곱은 (1,5)에 적혀있는 244이다.

그럼, 이제 최적 행렬곱이 나올 수 있는 행렬곱 순서를 알아보자.
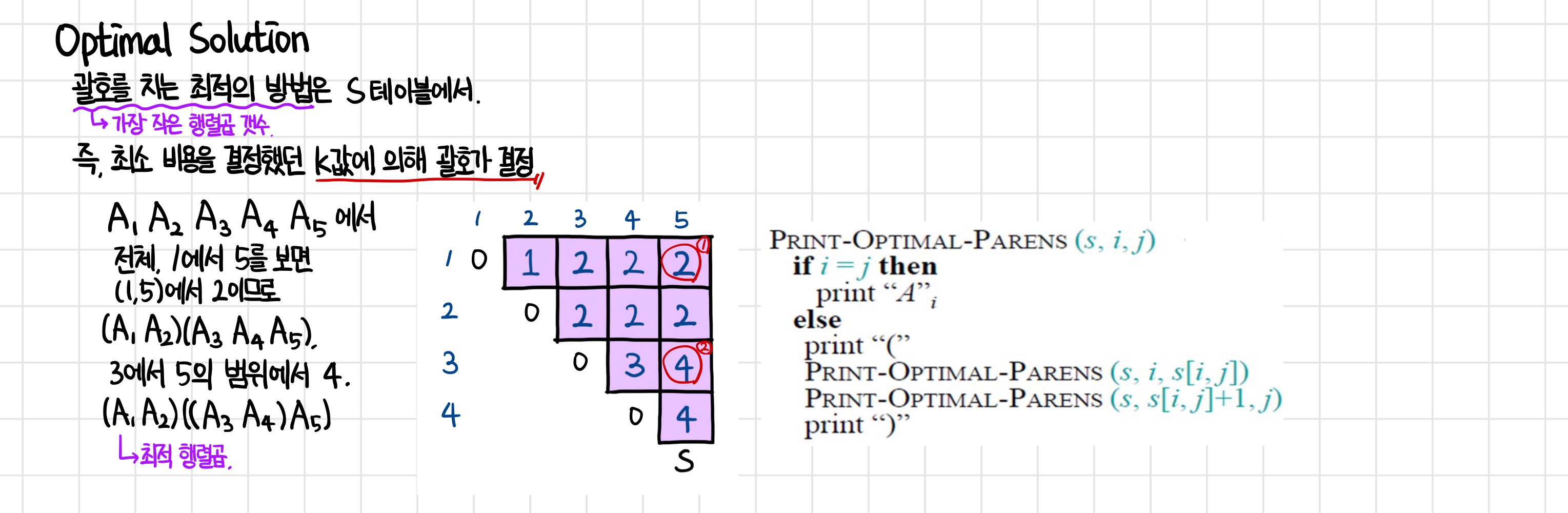
행렬곱 순서는 괄호에 의해 결정되는데, 이는 k값을 기록했던 s테이블에서 확인할 수 있다.
5개의 행렬이므로 A1에서 A5를 보면 (1,5)에서 s테이블의 값이 2이므로 두 번째 자리에서 끊어주면,
(A1 A2)(A3 A4 A5) - 이와 같은 형태가 된다.
그 따음, A1과 A2는 완성되었으므로 A3부터 A5를 s테이블에서 참조하면, 4번째 자리에서 괄호를 쳐줘야 하는 것을 알 수 있다.
따라서, 최종 결과는
(A1 A2)((A3 A4) A5) - 이렇게 된다.

해당 결과값을 출력하는 pseudocode이다.

'알고리즘 > DP' 카테고리의 다른 글
| [알고리즘] 편집 거리 문제 / Edit Distance Problem (0) | 2022.10.25 |
|---|---|
| [알고리즘] 최장 공통 부분수열 / LCS - Longest Common Subsequences (1) | 2022.10.23 |
| [알고리즘] Dynamic Programming (동적 계획법) (0) | 2022.10.11 |