
Longest Common Subsequence, 줄여서 LCS는 주어진 여러 수열의 공통 부분수열 중에서 가장 긴 수열을 찾는 문제이다. 아래 예시로, 수열 x와 y가 있다고 하자.
x는 ABCBDAB, y는 BDCABA일 때, 이 둘의 공통 수열은 매우 다양하지만, 그 중에서 가장 긴 수열은 BCBA이다.
이처럼 다양한 공통 수열 중에서 가장 긴 것을 찾는 문제이다.
문제 해결을 위하여 테이블을 구성하고, 일치하는 문자가 있을 경우 더해주는 방식의 DP를 사용했다.
DP, 동적 계획법에 대한 내용은 아래 링크에 자세하게 설명되어 있다.
[알고리즘] Dynamic Programming (동적 계획법)
동적 계획법, Dynamic Programming(DP)는 최적화 이론의 한 종류로, 특정 값을 구하기 위해서 다른 범위의 값을 이용해 효율적으로 값을 구하는 알고리즘으로, 쉽게 말해 답을 재활용하는 알고리즘이다
9-coding.tistory.com
필기 사진에 있는 코드를 보면, LCS는 최장 공통 부분수열을 담은 2차원 배열 테이블이고, max함수는 인수들 중에서 가장 큰 수를 반환하는 함수이다.
x 문자열의 i번째 문자와 y 문자열의 j번째 문자를 비교했을 때 일치하면, 테이블의 좌측 상단의 수에서 1을 더해 해당 위치에 저장하고, 일치하지 않는다면, 왼쪽 또는 위쪽 수를 그대로 [i][j] 위치에 저장하는 것을 구현한 코드이다.
아래에 예시를 통해 보면 해결 방법을 더 쉽게 이해할 수 있을 것이다.
Pseudocode

이 pseudocode는 LCS를 구현한 것으로, 위의 설명코드를 부연설명하기 위해 첨부해 보았다.
Time/Space Complexity

문자열의 길이를 m, n이라고 했을 때, 시간 복잡도와 공간 복잡도는 각 문자열의 길이를 곱한 것과 같다.
DP 테이블을 사용해 문제를 해결하는 것이므로, 각 문자열의 길이만큼의 테이블이 형성되기 때문에 시간/공간 복잡도는 테이블의 크기에 비례한다.
최장 공통 부분수열을 찾는 백트래킹의 경우, 두 문자열의 길이를 더한 것에 비례한다.

그럼 이제, 앞서 설명한 것을 바탕으로 테이블을 그려 LCS를 직접 구해보자.
두 문자열을 행과 열에 첫자리 공집합을 포함하여 적어주고, 첫 자리는 모두 0으로 초기화해준다.
상황은, 비교하는 문자열이 일치하는지, 일치하지 않는지로 구분된다.
가장 첫번째인 A와 B를 비교하는 자리에서는 두 문자가 일치하지 않으므로 왼쪽 또는 위쪽에서 큰 값을 가져와 그대로 옮겨적어준다.
그 다음, B와 B를 비교하는 자리에서는 두 문자가 일치하므로 대각선 왼쪽 위의 값에서 1을 추가해 그 자리에 적어준다.
이 과정을 계속 반복하여 빈칸을 모두 채워주면 된다.
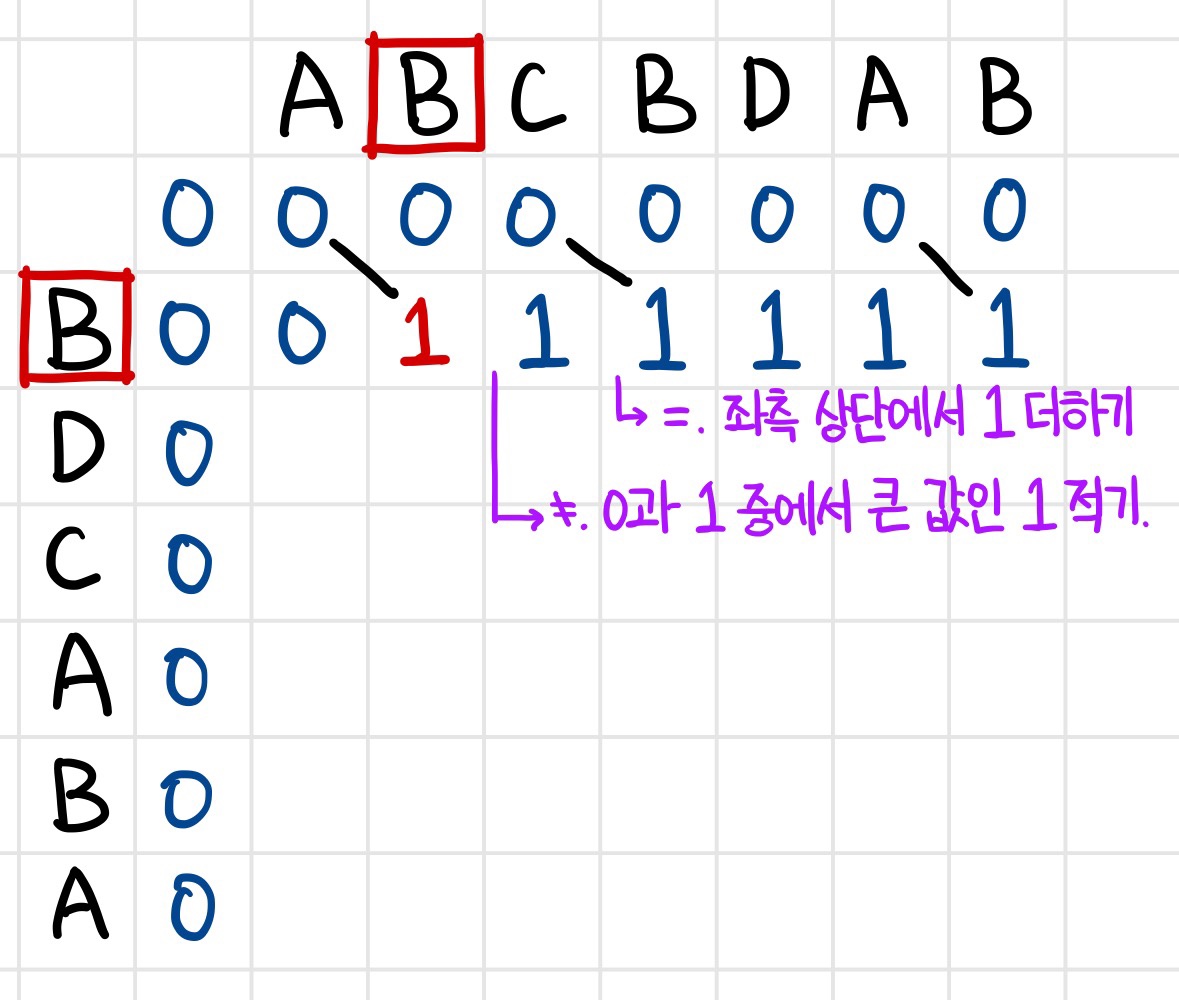
행을 모두 채웠을 때의 사진이다. 표에서 보이는 것처럼 문자열이 일치했던 자리에서는 대각선으로 선을 만들어준다.
마찬가지로 일치하지 않는 곳에서는 왼쪽/위쪽 값 중 큰 값을 적고, 일치하는 곳에서는 대각선 왼쪽 위에서 1을 더해 내려오기 때문에 계속 자리에 1이 적히는 것을 볼 수 있다.

반복적으로 해당 과정을 반복하여, DP테이블을 완성한 모습이다.
최장 공통 부분수열의 길이는 오른쪽 하단에 있으며, 해당 예제에서는 길이가 4인 수열이 최장 공통 부분수열임을 알 수 있다.

길이는 DP테이블의 최우측하단을 보면 알 수 있고, 그 문자열이 무엇인지 알기 위해서는 경로 추적(backtracking/backtracing)을 거쳐야 한다.
규칙은 다음과 같다.
1. 최우측하단, 정답이 쓰여있는 자리에서 같은 숫자일 때만
2. 왼쪽/위쪽으로만 이동하되,
3. 더 이상 같은 숫자가 없게 되면,
4. 대각선 왼쪽 위로 이동하여
5. 0이 나올 때까지 반복한다.
이 방법을 통해, 대각선 왼쪽 위로 가는 경우(문자열이 일치하는 경우)의 문자를 출력하면, 그 수열이 무엇인지 알 수 있다.
다만 뒤에서부터 찾아가는 방식이기 때문에 문자열을 뒤집어주는 과정이 필요하다.
그런데, 이 사진에서는 왼쪽으로 먼저 경로를 설정했지만, 위쪽으로 먼저 이동하게 되면 어떻게 될까?

이 사진처럼, 다른 조합의 문자열이 나온다.
LCS는 다양한 문자열이 나올 수 있는데, 최장 공통 부분수열이 나왔다고 하더라도, 같은 최장 길이를 가진 여러 문자열이 존재할 수 있다. 그것은 경로 추적을 어떤 방식으로 하느냐에 따라 구할 수 있는데, 경로를 추적할 때 왼쪽으로 먼저 갈지, 위쪽으로 먼저 갈지 정하는 등으로 구할 수 있다. 이전 사진에서는 왼쪽으로 먼저 가서 BCBA라는 결과가 나왔는데, 이 사진에서는 위쪽으로 먼저 이동해 BDAB라는 결과가 나왔다. 그리고, BCBA와 BDAB 모두 문자열의 길이는 4로 동일하다.
이처럼 LCS에서는 다양한 경우의 최장 부분 공통 문자열이 나올 수 있고, 그 길이는 모두 동일하다.

이 사진은 amputation과 spanking의 LCS를 구하기 위한 테이블이다.
위에서 설명한 내용을 익히고 난 다음, 직접 테이블을 채워보면서 개념을 잘 이해했는지 확인해보자.
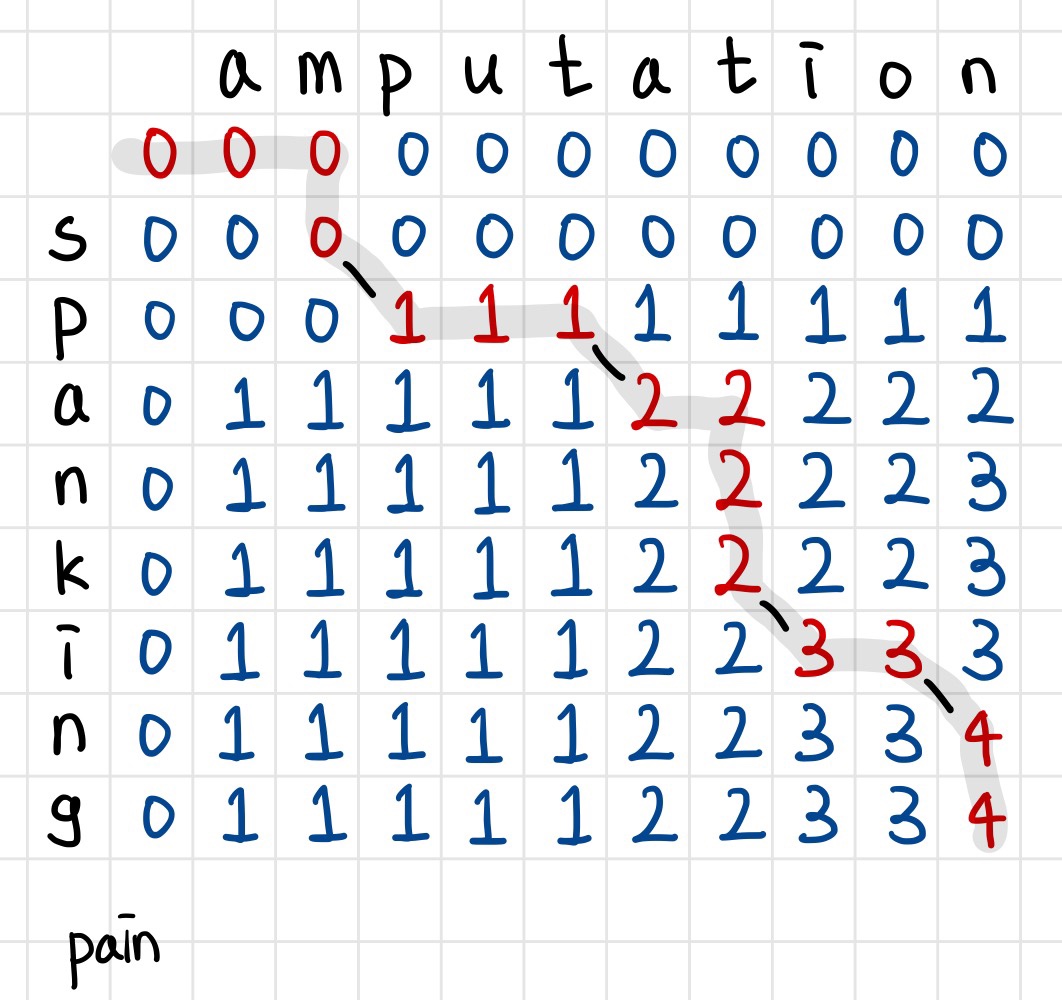
테이블을 완성한 모습이다. LCS 길이는 4, 문자열은 pain이다.
다음은 이 LCS 알고리즘을 백준을 통해 코드로 구현한 게시물이다.
[백준/BOJ-9251] LCS
LCS 9251번: LCS LCS(Longest Common Subsequence, 최장 공통 부분 수열)문제는 두 수열이 주어졌을 때, 모두의 부분 수열이 되는 수열 중 가장 긴 것을 찾는 문제이다. 예를 들어, ACAYKP와 CAPCAK의 LCS는 ACAK가 된
9-coding.tistory.com


'알고리즘 > DP' 카테고리의 다른 글
| [알고리즘] 연쇄 행렬 곱셈 / Matrix Chain Multiplication (0) | 2022.10.27 |
|---|---|
| [알고리즘] 편집 거리 문제 / Edit Distance Problem (0) | 2022.10.25 |
| [알고리즘] Dynamic Programming (동적 계획법) (0) | 2022.10.11 |