
편집 거리 문제, Edit Distance Problem은 하나의 문자열을 수정해 Insert/Delete/Copy(또는 Substitute)를 사용하여 최소한의 횟수/비용으로 다른 문자열로 변환하는 문제이다.
하나의 문자열을 최소 시행을 거쳐 다른 문자열로 변환하기 위해서는 copy라는 과정을 꼭 거쳐야 한다.
algorithm을 alligator로 바꾸는 예제를 살펴보자.
Insert/Delete/Copy를 적절히 사용하여 사진에서처럼 변환해주면, (회색은 아직 하지 않은 부분, 남색은 삽입, 빨간색은 삭제, 보라색은 복사) 14번의 시행으로 변환을 마칠 수 있다.

그렇다면, 이게 그냥 다 지우고 다시 쓰는 것과 무슨 차이가 있을까?
Copy를 사용해 문자열을 변환했을 경우에는 14번의 시행인데, algorithm과 alligator는 9글자이므로 모두 지우는데 9번, 다시 쓰는데 9번, 총 18회의 시행이 생긴다.이때 편집 거리 문제는 궁극적으로 최소한의 비용으로 문자열을 바꾸고자 하는 것인데, 비용이 주어질 때 일반적으로 삽입과 삭제의 비용이 복사 비용보다 월등히 높으므로 문자열 변환시 복사를 이용하는 것이 압도적으로 유리하고,바로 이 점이 편집 거리 문제를 구하는 이유이다.

삽입, 삭제, 복사하는 비용을 구하는 방법은 위의 코드와 같다.
ED라는 DP 테이블을 만들고, 이것을 이용하여 테이블을 모두 채워넣어준다.DP, 동적 계획법에 대한 내용은 아래 링크에 자세하게 설명되어 있다.
이 게시물에서는 예제로 삽입/삭제의 cost를 1, 복사의 cost를 0으로 두었지만, 문제에서 비용이 제시되었다면, 그 자리에 각 비용을 더해주면 된다.
삽입은 테이블 위쪽 값에서 비용을 더해주고, 삭제는 테이블의 왼쪽 값에서 비용을 더해주고, 복사는 대각선 위의 값을 그대로 적어준다. (비용이 있다면 비용 추가)
[알고리즘] Dynamic Programming (동적 계획법)
동적 계획법, Dynamic Programming(DP)는 최적화 이론의 한 종류로, 특정 값을 구하기 위해서 다른 범위의 값을 이용해 효율적으로 값을 구하는 알고리즘으로, 쉽게 말해 답을 재활용하는 알고리즘이다
9-coding.tistory.com

각 문자열에 맞추어 공집합을 포함해 테이블을 작성해준다.
"monkey"에서 "money"를 바꾸는 과정에서, monkey는 가로로, money는 세로로 적어준다.
기본적으로 테이블의 ED[0][0]은 0이고, ED[0][j]와 ED[i][0]은 행/열이 커질수록 1씩 더해주면서 초기화를 완료한다.
이 뜻은, 예시에서 볼 수 있듯 "mo"에서 공집합을 만드는 경우로 볼 수 있다. 그러기 위해선 두 번 지우는 과정이 필요하므로, 그 자리에 2를 적어준다.
마찬가지로, 세로 부분의 경우 공집합에서 money를 만드는 과정이므로 공집합에서 "m"을 만드는 과정은 삽입 1회, "mo"를 만드는 과정은 삽입 2회, "mon"을 만드는 과정은 삽입 3회, ... 이다.

m과 m처럼 비교하는 문자가 같으면 대각선 왼쪽 위의 값을 그대로 적어줍니다 (해당 예제에서 copy의 cost는 0)
비교하는 문자가 다를 경우에는 왼쪽이나 위 중에서 가장 작은 값에 1을 더해서 테이블에 적어줍니다.
여기서 의미하는 뜻은, "mo"에서 "m"을 만드는 과정에서 "o"를 삭제하는 것입니다.
그렇기 때문에 테이블에서도 왼쪽 값에서 1을 추가한, 즉 삭제를 한 과정이라는 과정임을 알 수 있습니다.
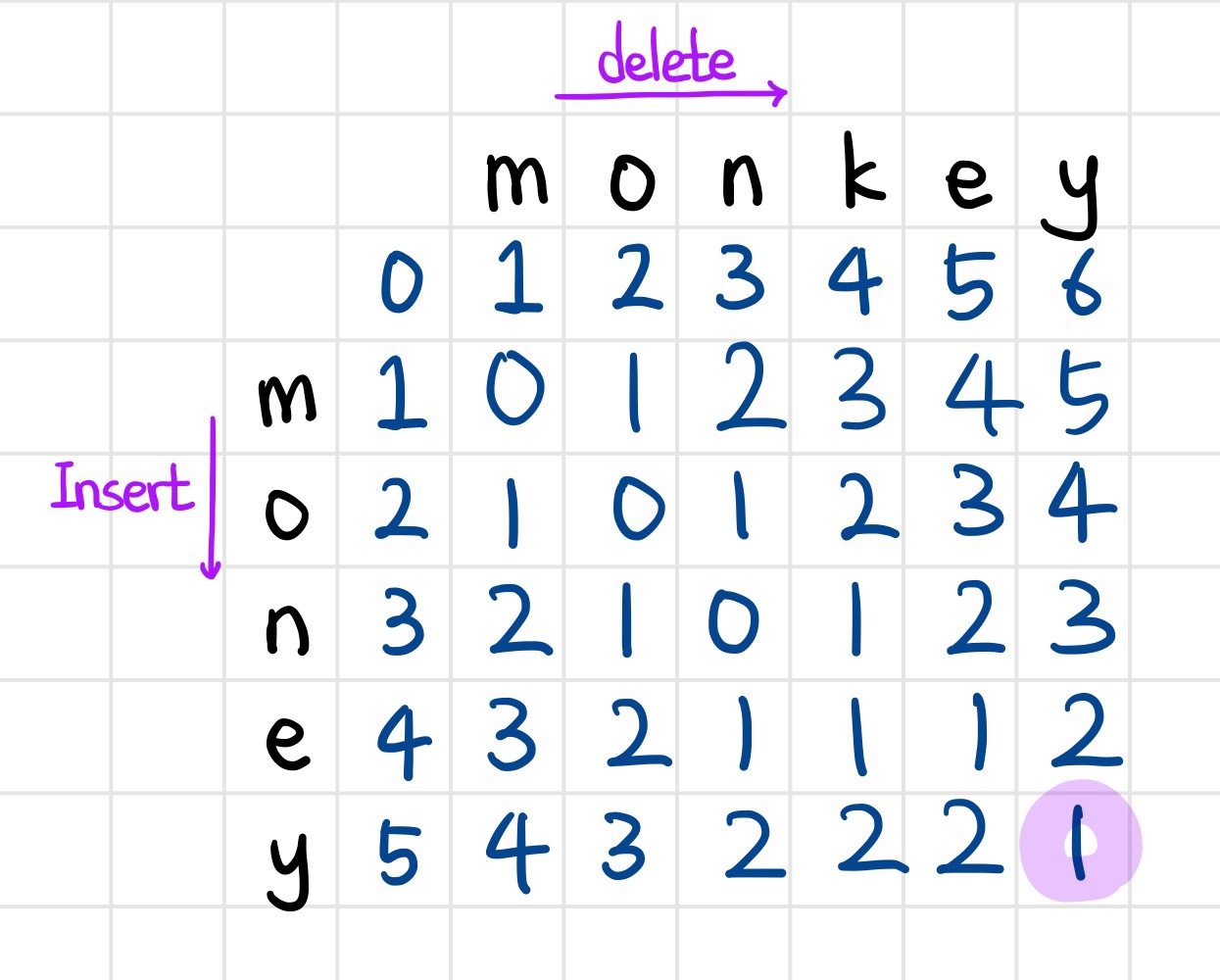
이 과정을 (그 자리에서 비교하는 문자가 같으면 대각선 왼쪽 위의 값, 다르면 왼쪽 또는 위쪽의 값에 비용을 더해주는 과정) 테이블을 모두 채울 때까지 반복해줍니다.
이렇게 테이블을 모두 채우면, 오른쪽 아래 마지막 값이 정답이 됩니다.

'알고리즘 > DP' 카테고리의 다른 글
| [알고리즘] 연쇄 행렬 곱셈 / Matrix Chain Multiplication (0) | 2022.10.27 |
|---|---|
| [알고리즘] 최장 공통 부분수열 / LCS - Longest Common Subsequences (0) | 2022.10.23 |
| [알고리즘] Dynamic Programming (동적 계획법) (0) | 2022.10.11 |